Born-Haber Cycles
This lesson covers:
- How Born-Haber cycles can be used to determine lattice enthalpies
- Calculating other values using Born-Haber cycles
- Comparing experimental and theoretical lattice enthalpies
- Ion polarisation and factors affecting it
Calculating lattice enthalpies with Born-Haber cycles
Hess' law states that the overall enthalpy change for a reaction is independent of the route taken.
As lattice enthalpies cannot be measured directly, Born-Haber cycles are used to determine the enthalpy change for an alternative, indirect pathway.
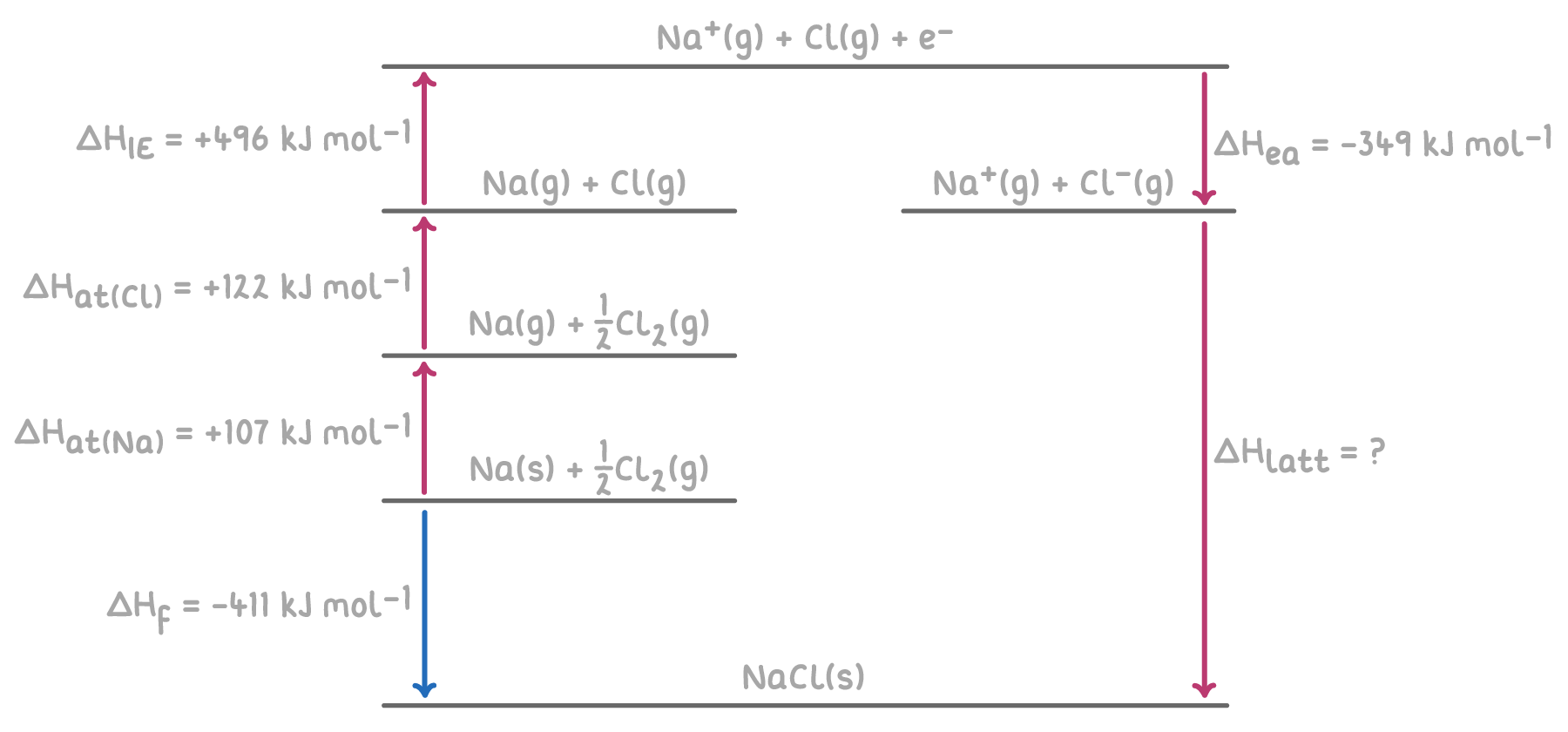
Here's an example of a Born-Haber cycle for calculating the lattice enthalpy of sodium chloride (NaCl).
Worked example 1 - Calculating lattice enthalpy of sodium chloride
Given the following enthalpy changes, calculate the lattice enthalpy of sodium chloride (NaCl) using a hypothetical Born-Haber cycle:
| Enthalpy change | Value (kJ mol-1) |
|---|---|
| Enthalpy of formation of NaCl, ∆Hf | -411 |
| Enthalpy of atomisation of sodium, ∆Hat(Na) | +107 |
| Enthalpy of atomisation of chlorine, ∆Hat(Cl) | +122 |
| First ionisation energy of sodium, ∆HIE1(Na) | +496 |
| Electron affinity of chlorine, ∆Hea(Cl) | -349 |
Step 1: Apply Hess's Law for the Born-Haber cycle
The overall enthalpy change for the formation of NaCl can be calculated by summing the enthalpy changes for each step of the Born-Haber cycle.
Step 2: Substitution and correct evaluation
ΔHlatt(NaCl) = -ΔHea(Cl) - ΔHIE1(Na) - ΔHat(Cl) - ΔHat(Na) + ΔHf
= -(-349) - 496 - 122 - 107 + (-411)
= 349 - 496 - 122 - 107 - 411
ΔHlatt(NaCl) = -787 kJ mol-1
Therefore, the lattice enthalpy of sodium chloride is -787 kJ mol-1.
Adapting Born-Haber cycles for different compounds
The Born-Haber cycle can be modified for various compounds.
For example, when calculating the lattice enthalpy of a group 2 compound like magnesium chloride (MgCl2), extra steps are needed:
- Magnesium forms a 2+ ion, so the second ionisation energy of magnesium is included.
- There are 2 moles of chlorine per mole of MgCl2, so the atomisation enthalpy of chlorine is doubled.
Similarly, when constructing a Born-Haber cycle for sodium oxide (Na2O), additional steps are required:
- There are 2 moles of sodium per mole of Na2O, so the atomisation enthalpy and first ionisation energy of sodium are doubled.
- Oxygen forms a 2- ion, so the second electron affinity of oxygen is included.
For compounds with ions that have charges greater than 1, additional ionisation energies and electron affinities are incorporated into the Born-Haber cycle, as demonstrated in the following examples.
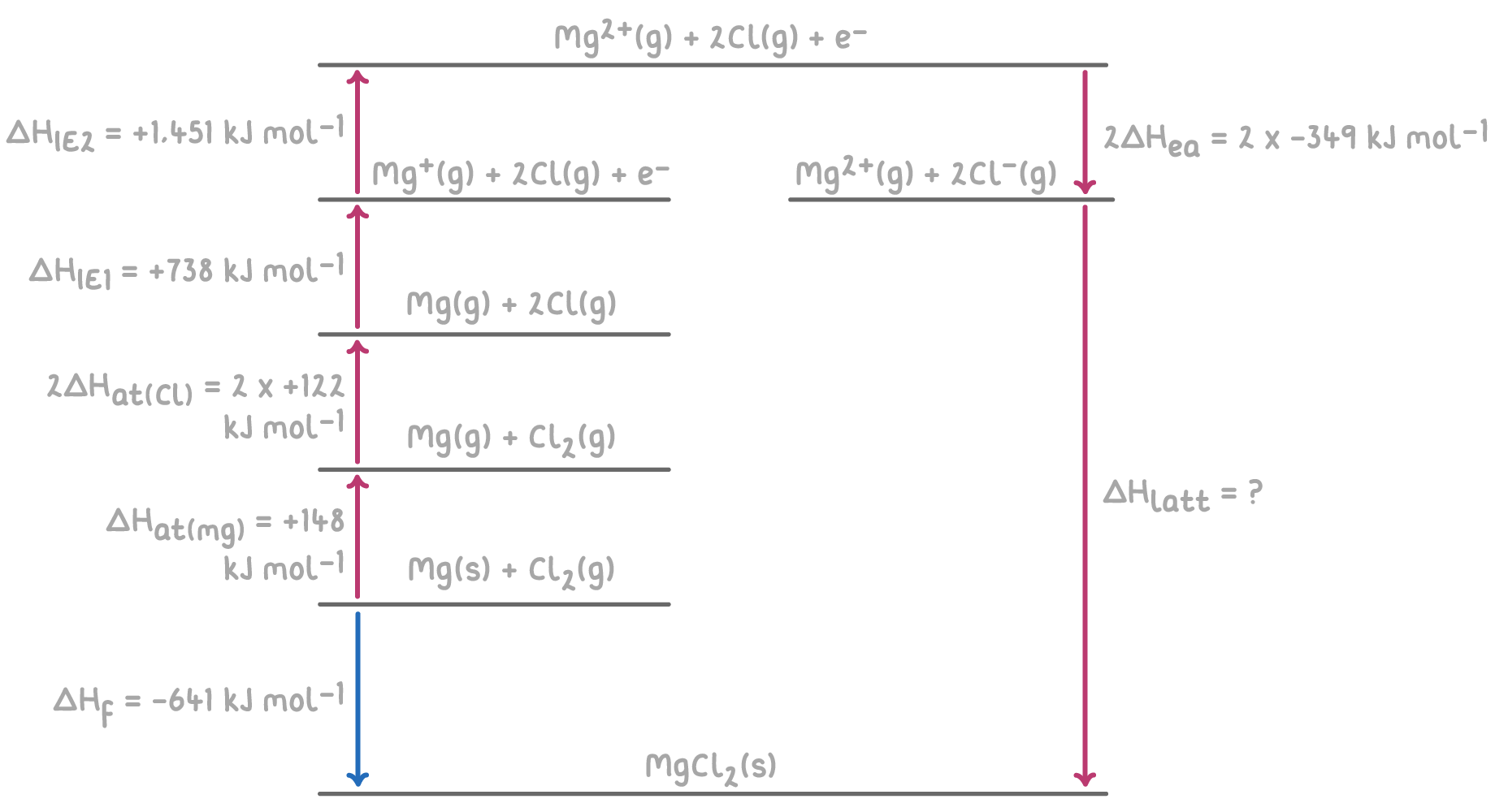
Worked example 2 - Calculating lattice enthalpy of magnesium chloride
Given the following enthalpy changes, calculate the lattice enthalpy of magnesium chloride (MgCl2) using a hypothetical Born-Haber cycle:
| Enthalpy change | Value (kJ mol-1) |
|---|---|
| Enthalpy of formation of MgCl2, ∆Hf | -641 |
| Atomisation enthalpy of magnesium, ∆Hat(Mg) | +148 |
| Atomisation enthalpy of chlorine, ∆Hat(Cl) | +122 |
| First ionisation energy of magnesium, ∆HIE1(Mg) | +738 |
| Second ionisation energy of magnesium, ∆HIE2(Mg) | +1,451 |
| Electron affinity of chlorine, ∆Hea(Cl) | -349 |
Step 1: Apply Hess's law for the Born-Haber cycle
The overall enthalpy change for the formation of MgCl2 can be calculated by summing the enthalpy changes for each step of the Born-Haber cycle.
Step 2: Substitution and correct evaluation
ΔHlatt(MgCl2)=−2ΔHea(Cl)−ΔHIE1(Mg)−ΔHIE2(Mg)−2ΔHat(Cl)−ΔHat(Mg)+ΔHf
=−(−698)−738−1,451−244−148+(−641)
=698−738−1,451−244−148−641
ΔHlatt(MgCl2)=−2,524 kJ mol−1
Therefore, the lattice enthalpy of magnesium chloride is -2,524 kJ mol-1.
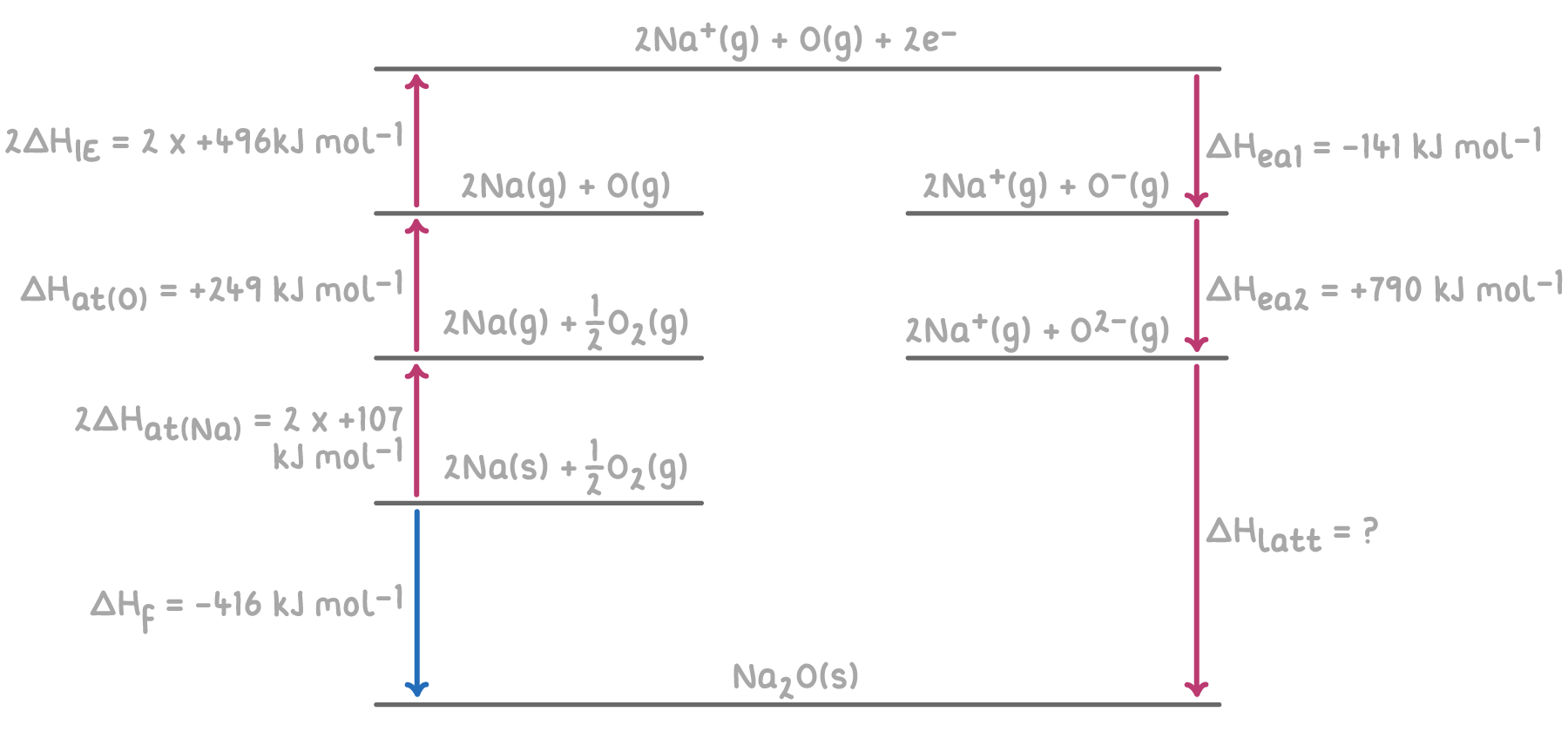
Worked example 3 - Calculating lattice enthalpy of sodium oxide
Given the following enthalpy changes, calculate the lattice enthalpy of sodium oxide (Na2O) using a hypothetical Born-Haber cycle:
| Enthalpy change | Value (kJ mol-1) |
|---|---|
| Enthalpy of formation of Na2O, ∆Hf | -416 |
| Atomisation enthalpy of sodium, ∆Hat(Na) | +107 |
| Atomisation enthalpy of oxygen, ∆Hat(O) | +249 |
| First ionisation energy of sodium, ∆HIE1(Na) | +496 |
| First electron affinity of oxygen, ∆Hea1(O) | -141 |
| Second electron affinity of oxygen, ∆Hea2(O) | +790 |
Step 1: Apply Hess's law for the Born-Haber cycle
The overall enthalpy change for the formation of Na2O can be calculated by summing the enthalpy changes for each step of the Born-Haber cycle.
Step 2: Substitution and correct evaluation
ΔHlatt(Na2O)=−ΔHea1(O)−ΔHea2(O)−2ΔHIE1(Na)−2ΔHat(Na)−ΔHat(O)+ΔHf
= -(-141) - 790 - 992 - 214 - 249 + (-416)
= 141 - 790 - 992 - 214 - 249 - 416
ΔHlatt(Na2O) = -2,520 kJ mol-1
Therefore, the lattice enthalpy of sodium oxide is -2,520 kJ mol-1.
Born-Haber cycles can calculate various enthalpy and energy values
Born-Haber cycles are versatile and can be used to determine any unknown enthalpy or energy value within the cycle. The process is similar to calculating lattice enthalpy.
For instance, here's an example of a Born-Haber cycle for calculating the enthalpy of formation of magnesium oxide (MgO).
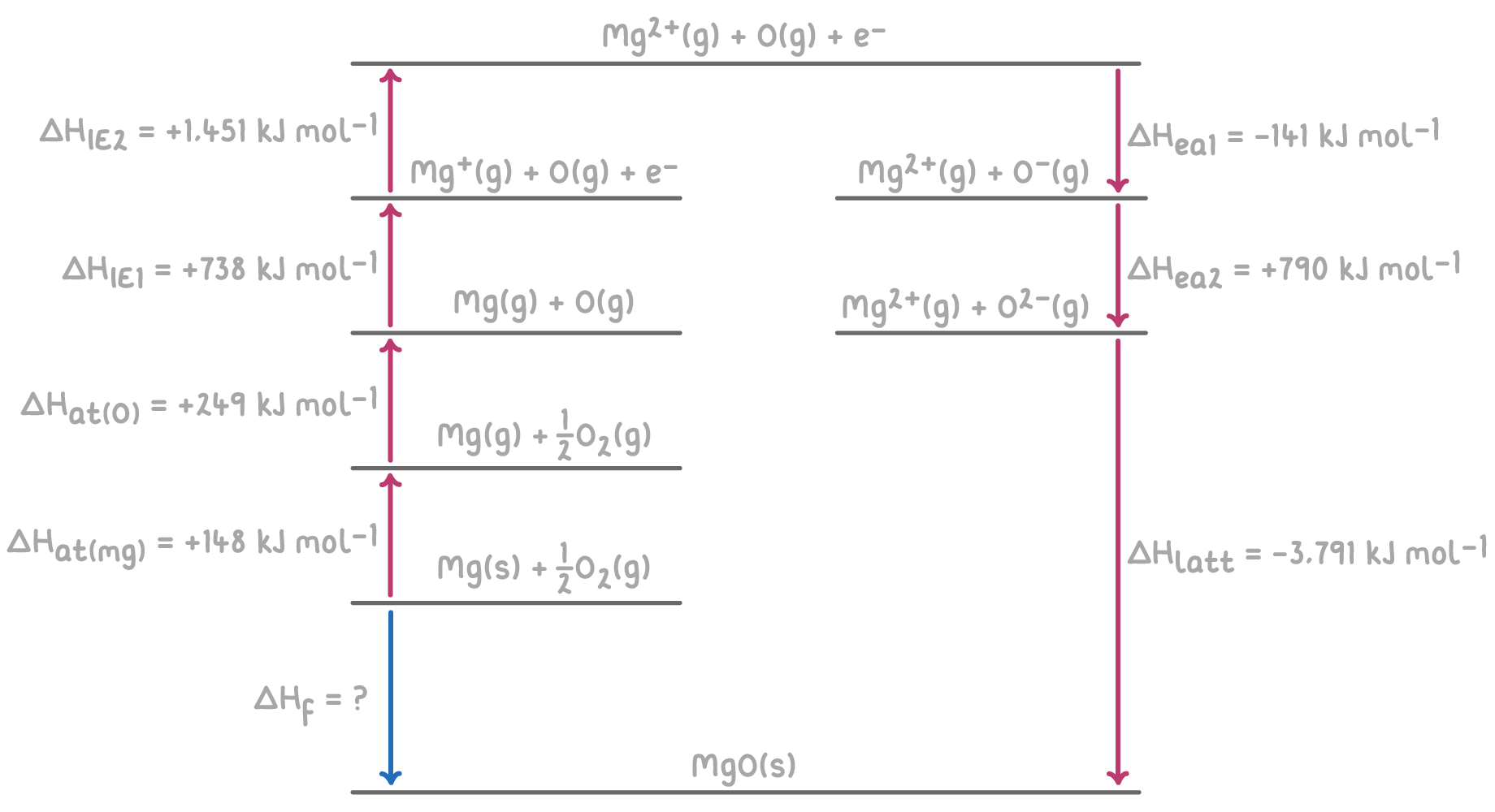
Worked example 4 - Calculating the enthalpy of formation of magnesium oxide
Given the following enthalpy changes, calculate the enthalpy of formation (ΔHf) of magnesium oxide (MgO) using a hypothetical Born-Haber cycle:
| Enthalpy change | Value (kJ mol-1) |
|---|---|
| Lattice enthalpy of MgO, ∆Hlatt | -3,791 |
| Atomisation enthalpy of magnesium, ∆Hat(Mg) | +148 |
| Atomisation enthalpy of oxygen, ∆Hat(O) | +249 |
| First ionisation energy of magnesium, ∆HIE1(Mg) | +738 |
| Second ionisation energy of magnesium, ∆HIE2(Mg) | +1,451 |
| First electron affinity of oxygen, ∆Hea1(O) | -141 |
| Second electron affinity of oxygen, ∆Hea2(O) | +790 |
Step 1: Applying Hess's law for the Born-Haber cycle
The overall enthalpy change for the formation of MgO can be calculated by summing the enthalpy changes for each step of the Born-Haber cycle.
Step 2: Substitution and correct evaluation
ΔHf=ΔHat(Mg)+ΔHat(O)+ΔHIE1(Mg)+ΔHIE2(Mg)+ΔHea1(O)+ΔHea2(O)+ΔHlatt
= 148 + 249 + 738 + 1,451 + (-141) + 790 + (-3,791)
= 148 + 249 + 738 + 1,451 - 141 + 790 - 3,791
ΔHf = -556 kJ mol-1
Therefore, the enthalpy of formation of magnesium oxide is -556 kJ mol-1.
Ion polarisation explains why experimental lattice enthalpies often differ from theoretical values
Theoretical lattice enthalpies are calculated using a purely ionic model, which assumes that all ions are spherical with evenly distributed charge. However, experimental values often deviate from these predictions, indicating that most ionic compounds have some covalent character. This disparity arises due to a phenomenon called ion polarisation.

- In an ionic lattice, the positive charge on the cation may attract the electrons in the anion towards it, resulting in a distortion of the anion's electron cloud.
- This distortion causes the anion to lose its spherical shape, a process known as ion polarisation.
- Greater polarisation leads to more covalent bonding, which explains why experimental lattice enthalpies often differ from theoretical values.
Comparing lattice enthalpies reveals the extent of ionic bonding
The difference between experimental and theoretical lattice enthalpies provides insight into the nature of bonding in ionic lattices. A larger difference suggests stronger polarisation and more covalent character, while a smaller difference indicates a more purely ionic compound.
To illustrate this concept, let's compare the experimental and theoretical lattice enthalpy values for magnesium chloride (MgCl2) and sodium chloride (NaCl):
For magnesium chloride, the experimental lattice enthalpy (-2,524 kJ mol-1) is significantly more negative than the theoretical value (-2,326 kJ mol-1), suggesting stronger bonding than predicted by the purely ionic model. The small, highly charged Mg2+ cation strongly polarises the Cl- anions, resulting in significant covalent character.