Entropy

This lesson covers: 

1. What entropy is and how it relates to disorder
2. The factors that affect entropy
3. How entropy influences reaction feasibility
4. Calculating entropy changes for reactions

Entropy is a measure of disorder

Entropy (S) is a thermodynamic quantity that measures the degree of disorder or randomness in a system. It quantifies the number of ways particles can be arranged and how energy is distributed among those particles.

Key points about entropy:

• A high entropy value indicates a high level of disorder.
• Entropy is always positive and increases as disorder increases.
• Systems naturally tend towards states of higher entropy.

Factors affecting entropy

Three factors influence the entropy of a substance:

1.   Physical state

The physical state of a substance impacts its entropy:

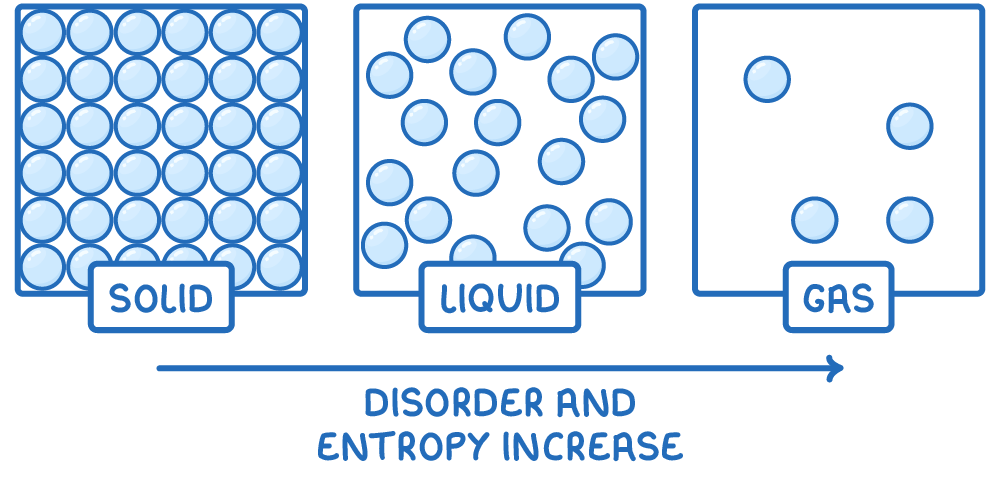
• Solids have the lowest entropy because their particles are held in fixed positions, resulting in a highly ordered structure.
• Liquids have higher entropy than solids as their particles have more freedom to move, introducing some disorder.
• Gases have the highest entropy due to the random motion and wide spacing of their particles, resulting in the most disordered arrangement.

2.   Number of particles

Entropy increases with the number of particles in a system. More particles allow for a greater number of possible arrangements and energy distributions.

For example, in the reaction N₂O_4(g) ➔ 2NO_2(g), the number of moles of gas doubles from reactants to products. This increase in the number of particles results in an increase in entropy.

3.   Temperature

Higher temperatures increase entropy due to the increased kinetic energy and molecular motion of particles. At higher temperatures, particles have more energy and can access a greater number of disordered arrangements.

Entropy and reaction feasibility

Particles naturally tend towards more disordered states, as increased entropy provides greater energetic stability. This drive for disorder can make certain reactions feasible (able to proceed spontaneously) even when the enthalpy change is endothermic.

For example, the reaction between sodium hydrogencarbonate and hydrochloric acid is endothermic but still feasible:

NaHCO_3(s) + HCl_(aq) ➔ NaCl_(aq) + CO_2(g) + H₂O_(l)

The reaction produces gaseous carbon dioxide and liquid water, which have higher entropy than the solid reactant. This entropy increase overcomes the endothermic enthalpy change, making the reaction possible.

Calculating entropy changes for reactions

During a reaction, the entropy change (ΔS) between reactants and products can be calculated using the formula:

ΔS = S_products - S_reactants

Where:

• S_products is the sum of the standard entropies of all products
• S_reactants is the sum of the standard entropies of all reactants

Standard entropy (S^⦵) is the entropy of 1 mole of a substance under standard conditions (100 kPa pressure and 298 K temperature). Its units are J K^-1 mol^-1.

The steps for calculating ΔS of a reaction are:

1. Find the sum of standard entropies for the products (ΣS^⦵(products)).
2. Find the sum of standard entropies for the reactants (ΣS^⦵(reactants)).
3. Subtract the sum of reactant entropies from the sum of product entropies.

If the balanced equation has coefficients other than 1, multiply the standard entropy of each substance by its coefficient.

Worked example 1 - Calculating entropy change for a reaction

Calculate the entropy change for the reaction where hydrogen chloride reacts with ammonia to produce ammonium chloride at standard conditions:

HCl_(g) + NH_3(g) ➔ NH₄Cl_(s)

Given:

• S^⦵[HCl_(g)] = 186.9 J K^-1 mol^-1
• S^⦵[NH_3(g)] = 192.8 J K^-1 mol^-1
• S^⦵[NH₄Cl_(s)] = 94.6 J K^-1 mol^-1

Step 1: Calculate the entropy of the products

S_products = S^⦵[NH₄Cl] = 94.6 J K^-1 mol^-1

Step 2: Calculate the entropy of the reactants

S_reactants = S^⦵[HCl] + S^⦵[NH₃]

= 186.9 + 192.8 = 379.7 J K^-1 mol^-1

Step 3: Equation

ΔS = S_products - S_reactants

Step 4: Substitution and correct evaluation

ΔS = 94.6 - 379.7 = -285.1 J K^-1 mol^-1

The negative ΔS indicates a decrease in entropy, meaning the system becomes more ordered as two gases combine to form a solid.

Worked example 2 - Calculating entropy change for a reaction

Calculate the entropy change for the reaction where carbon monoxide reacts with hydrogen to produce methanol at standard conditions:

CO_(g) + 2H_2(g) ➔ CH₃OH_(l)

Given:

• S^⦵[CO_(g)] = 197.7 J K^-1 mol^-1
• S^⦵[H_2(g)] = 130.7 J K^-1 mol^-1
• S^⦵[CH₃OH_(l)] = 126.8 J K^-1 mol^-1

Step 1: Calculate the entropy of the products

S_products = S^⦵[CH₃OH] = 126.8 J K^-1 mol^-1

Step 2: Calculate the entropy of the reactants

S_reactants = S^⦵[CO₂] + 2 x S^⦵[H₂]

=197.7+(2×130.7)=459.1 J K−1 mol−1

Step 3: Equation

ΔS = S_products - S_reactants

Step 4: Substitution and correct evaluation

ΔS = 126.8 - 459.1 = -332.3 J K^-1 mol^-1

The negative ΔS indicates a decrease in entropy, meaning the system becomes more ordered as gases combine to form a liquid.

Worked example 3 - Calculating entropy change for a reaction

Calculate the entropy change for the complete combustion of propane (C₃H₈) in oxygen to produce carbon dioxide and water vapor at standard conditions:

C₃H_8(g) + 5O_2(g) ➔ 3CO_2(g) + 4H₂O_(g)

Given:

• S^⦵[C₃H_8(g)] = 269.9 J K^-1 mol^-1
• S^⦵[O_2(g)] = 205.0 J K^-1 mol^-1
• S^⦵[CO_2(g)] = 213.7 J K^-1 mol^-1
• S^⦵[H₂O_(g)] = 188.7 J K^-1 mol^-1

Step 1: Calculate the entropy of the products

S_products = 3 x S^⦵[CO₂] + 4 x S^⦵[H₂O]

=(3×213.7)+(4×188.7)=1,395.9 J K−1 mol−1

Step 2: Calculate the entropy of the reactants

S_reactants = S^⦵[C₃H₈] + 5 x S^⦵[O₂]

=269.9+(5×205.0)=1,294.9 J K−1 mol−1

Step 3: Equation

ΔS = S_products - S_reactants

Step 4: Substitution and correct evaluation

ΔS = 1395.9 - 1294.9 = 101.0 J K^-1 mol^-1

The positive ΔS indicates an increase in entropy, showing the system becomes more disordered as the combustion of propane proceeds, which is attributed to the increase in the number of gas moles produced (7 moles of gaseous products from 6 moles of gaseous reactants).