The Arrhenius Equation

This lesson covers: 

1. What the Arrhenius equation is
2. How activation energy and temperature affect the rate constant
3. Calculations using the Arrhenius equation
4. Calculations involving Arrhenius plots

The Arrhenius equation links reaction rate to temperature and activation energy

The Arrhenius equation is a mathematical formula that connects the rate constant (k) of a chemical reaction with the temperature (T) and the activation energy (E_a). This equation helps us understand how these factors affect the rate of a chemical reaction.

The Arrhenius equation is given by:

k = Ae(RT−Ea​​)

Where:

• k = rate constant
• A = pre-exponential factor (also known as the Arrhenius constant)
• e = mathematical constant (the base of natural logarithms)
• E_a = activation energy (J mol^-1)
• R = gas constant (8.31 J K^-1 mol^-1)
• T = temperature (K)

Influence of activation energy and temperature on reaction rate

The Arrhenius equation reveals important relationships between the rate constant, activation energy, and temperature:

1. Activation energy (E_a):

• The higher the E_a, the lower the rate constant (k) becomes.
• A high activation energy means that fewer reactant molecules have sufficient kinetic energy to overcome the energy barrier and react successfully.
• Consequently, a reaction with a high E_a will have a slower rate.

2. Temperature (T):

• An increase in temperature leads to an exponential increase in the rate constant (k).
• At higher temperatures, reactant molecules move faster, resulting in more frequent collisions.
• Additionally, higher temperatures provide greater kinetic energy to reactant molecules, allowing a higher proportion to exceed the activation energy barrier.
• Both of these factors contribute to the increased reaction rate when temperature increases.

Notably, even a small temperature increase causes a large increase in rate due to the significantly higher fraction of molecules that have energies greater than, or equal to, E_a. Consequently, a much higher proportion of collisions become successful and reaction rate increases considerably. 

Calculating rate constants and activation energies

To calculate either the rate constant (k) or activation energy (E_a) when other variables are known, we often use the logarithmic form of the Arrhenius equation:

ln(k)=−RTEa​​+ln(A)

This equation represents a straight line where:

• y =ln(k)
• x =T1​
• Gradient =−REa​​
• y-interpect = ln(A)

Worked example 1 - Calculating activation energy

The decomposition of dinitrogen pentoxide (N₂O₅) at 310 K has a rate constant of 2.50×10−3 s−1. The Arrhenius constant for this reaction is 6.90×1012 s−1.

Calculate the activation energy, in kJ mol^-1, for this reaction, given R = 8.31 J K^-1 mol^-1.

Step 1: Logarithmic form of the Arrhenius equation

ln(k)=RT−Ea​​+ln(A)

Step 2: Rearrange equation to solve for E_a

Ea​=(ln(A)−ln(k))× RT

Step 3: Substitution and correct evaluation

Ea​=(ln(6.90×1012)−ln(2.50×10−3))×8.31×310

=35.6×8.31×310=91,600 J mol−1

Step 4: Conversion from J mol^-1 to kJ mol^-1

To convert from J mol^-1 to kJ mol^-1, divide by 1,000.

91,600 J mol^-1 = 91.6 kJ mol^-1

Therefore, the activation energy for the decomposition of N₂O₅ is 91.6 kJ mol^-1.

Using Arrhenius plots to determine activation energy and the Arrhenius constant

An Arrhenius plot graphs the logarithmic form of the Arrhenius equation, plotting ln k against T1​.

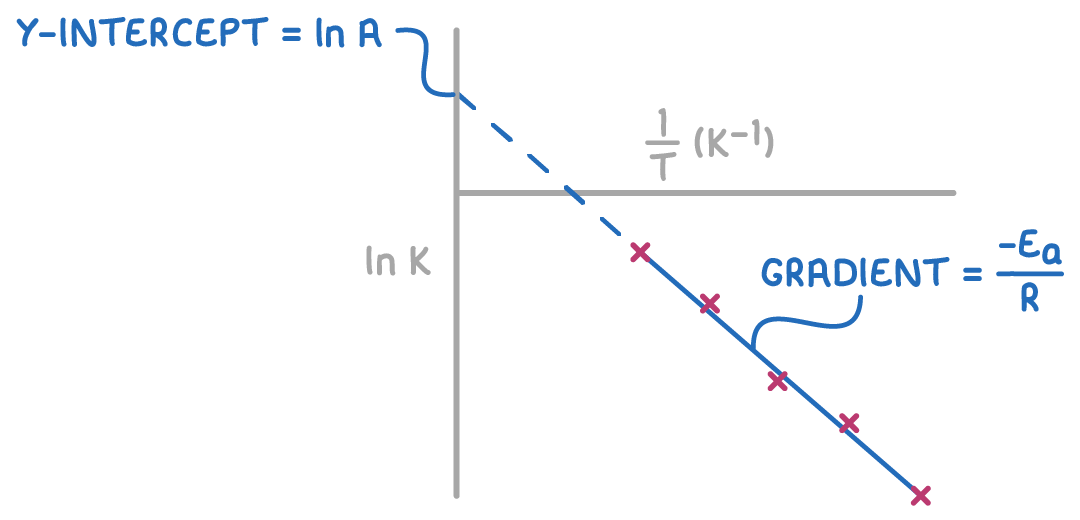
This yields a straight line from which we can determine:

1. Gradient - R−Ea​​, allowing us to calculate E_a.
2. y-intercept - ln A, which lets us find A by taking the exponential (e^intercept).

Worked example 2 - Calculating the activation energy and pre-exponential factor

Calculate the activation energy (J mol^-1) and pre-exponential factor from the Arrhenius plot below.

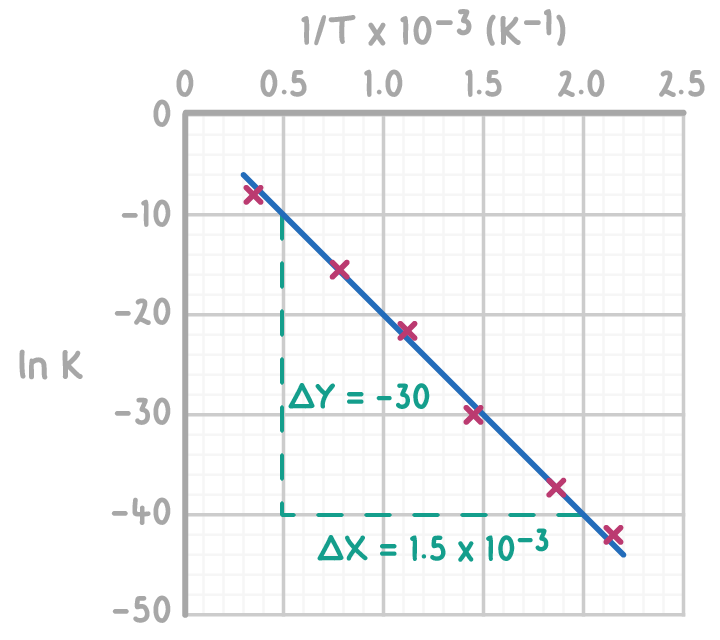
Step 1: Calculate the gradient of the line

Gradient =(2.0×10−3)−(0.5×10−3)−40−(−10)​

=(1.5×10−3)−30​=−20,000

Step 2: Calculate activation energy (E_a)

Ea​=−Gradient × R =−20,000×8.31=166,200 J mol−1

Step 3: Rearrange logarithmic form of the Arrhenius equation

ln(A)=RTEa​​+ln(k)

Step 4: Substitution and correct evaluation

Using the point (0.5 x 10^-3, -10) and the calculated gradient from step 1

ln(A)=(20,000×(0.5×10−3))−10

= 10 - 10 = 0

Step 5: Calculate pre-exponential factor (A)

A = e⁰ = 1.0

Therefore, the activation energy is 170,000 J mol^-1 and the pre-exponential factor is 1.0 dm³ mol^-1 s^-1.