Measuring Enthalpy Changes

This lesson covers: 

1. How calorimetry allows us to measure enthalpy changes
2. Using calorimetry to find the enthalpy change of combustion
3. Using calorimetry to find enthalpy changes during reactions in solution
4. Creating a temperature-time graph to accurately measure temperature change
5. Calculating enthalpy change using q = mcΔT

Measuring enthalpy changes with calorimetry

We can measure the energy transferred in a reaction as heat using an apparatus called a calorimeter. This allows us to determine enthalpy changes for reactions.

There are two main types of calorimetry experiments:

1. Combustion calorimetry - used to find the enthalpy change when a fuel is burned
2. Solution calorimetry - used to find enthalpy changes for reactions occurring in aqueous solutions

Combustion calorimetry

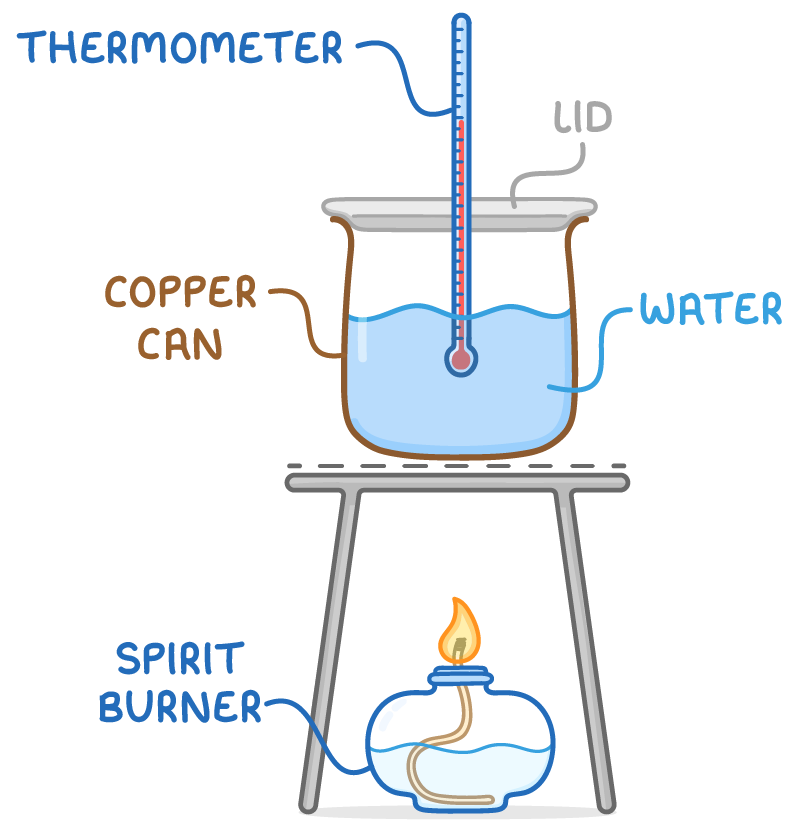
To find the enthalpy change of combustion:

1. A weighed fuel sample is burnt underneath a metal canister (calorimeter) containing a known mass of water.
2. As the fuel combusts, heat is transferred to the water. A thermometer measures the temperature change.
3. The temperature change along with the mass and heat capacity of water are used to calculate the heat energy.

Understanding inaccuracies in enthalpy change

In calorimetry, inaccuracies can lead to deviations in the measured enthalpy change. Generally, these errors result in an underestimation of the true enthalpy change.

Common sources of error

1. Heat loss - Heat escaping to the surroundings means less is absorbed by the water, leading to a lower measured enthalpy change.
2. Incomplete combustion - When fuel doesn't burn completely, less heat is produced, resulting in a lower calculated enthalpy change.
3. Fuel evaporation - If some fuel evaporates before burning, it reduces the amount of heat generated, thereby decreasing the measured enthalpy change.

Solution calorimetry

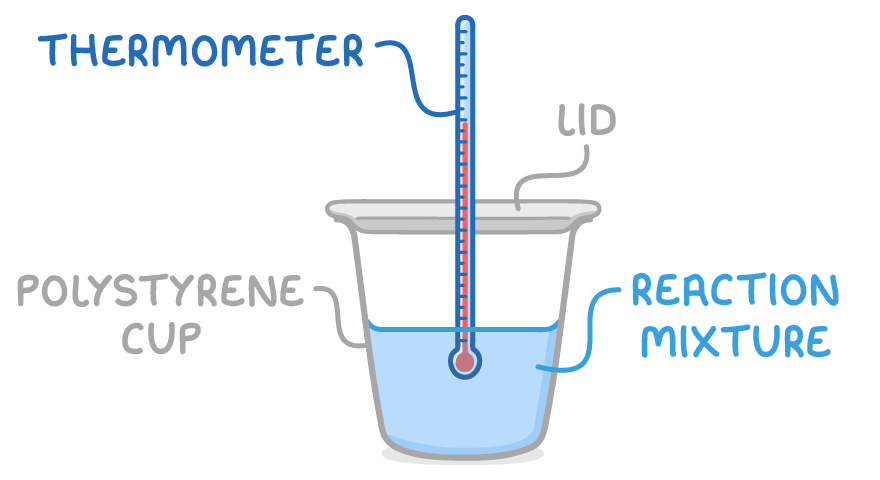
Solution calorimetry can find enthalpy changes for reactions occurring in aqueous solutions, including:

• Neutralisation
• Dissolution
• Displacement

The steps are:

1. Add a measured volume of one reactant to a polystyrene cup calorimeter and record initial temperature. 
2. Add a measured volume of a second reactant and quickly seal the container with a lid.
3. Carefully stir the mixture with the thermometer and record temperatures at regular intervals over time as heat is released or absorbed.

Polystyrene cups are used as the calorimeter for solution calorimetry instead of glass beakers because polystyrene is a better insulator, lightweight, waterproof, and has a low specific heat capacity. These properties reduce heat loss to the surroundings and minimise the amount of heat absorbed by the calorimeter itself.

Creating an accurate temperature-time graph

During a calorimetry experiment, the temperature fluctuates throughout - increasing rapidly as heat is released, reaching a peak, then decreasing gradually again.

If we just subtracted the final and initial values, we would underestimate the temperature change by missing the peak and not accounting for heat lost while measuring.

To accurately determine the temperature change:

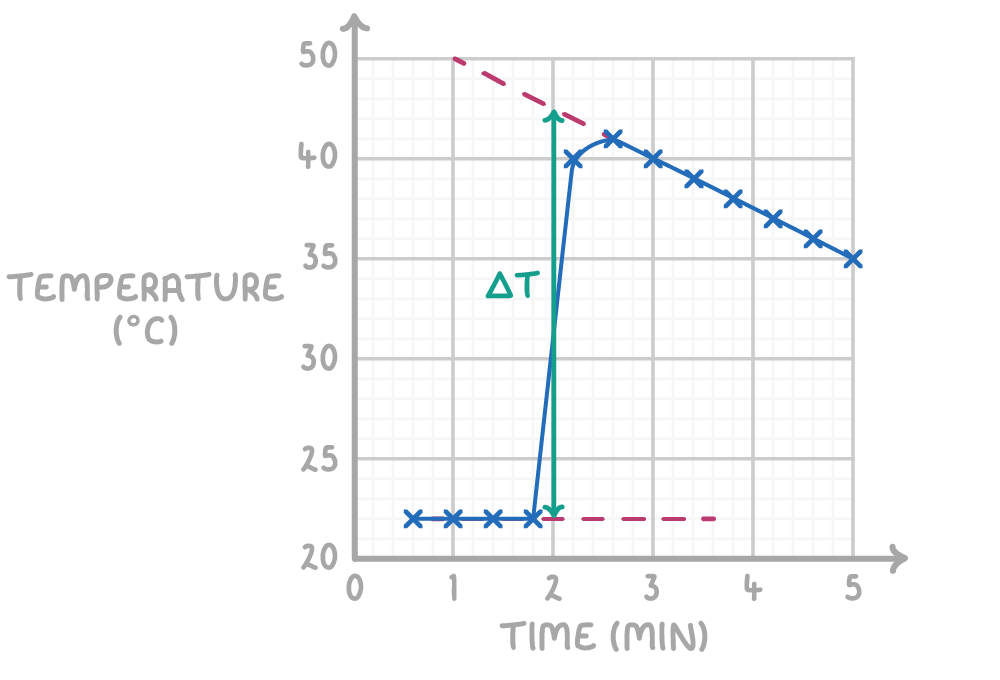
1. Plot the data - Begin by plotting the recorded temperature against time.
2. Establish baseline - Draw a line of best fit for the initial temperature readings before the reaction commences. This is your baseline.
3. Post-reaction line - After the peak reaction temperature is reached, draw another line of best fit for the cooling period.
4. Extrapolation - Extend both lines to intersect at the reaction's start time.
5. True temperature change - The difference between the two extrapolated lines of best fit at the start of the reaction gives the accurate temperature change.

Calculating enthalpy change

To measure enthalpy changes in chemical reactions, you need to use two key equations sequentially: first to calculate the heat energy change, and then to use that value to calculate the enthalpy change per mole.

First, the heat energy change can be calculated using the equation:

q = mcΔT

Where:

• q = heat energy (J)
• m = mass of water or solution (g)
• c = specific heat capacity of water, 4.18 J g^-1 K^-1
• ΔT = temperature change (K)

The official unit for ΔT is Kelvin (K). However, the Celsius scale gives the same numerical temperature change, so °C can also be used.

Next, use the value of q obtained from the first equation to find the enthalpy change with the equation:

ΔH =−nq​

Where:

• ΔH = enthalpy change (kJ mol^-1)
• q = heat energy (kJ)
• n = number of moles of the substance (mol)

Enthalpy changes are typically expressed in kJ mol^-1 so you need to convert q from J to kJ by dividing by 1,000 before using it in the second equation.

Worked example 1 - Calculating standard enthalpy of combustion

In a laboratory experiment, 1.45 g of an organic liquid fuel (M_r = 58.0) were completely burned in oxygen. The heat formed during this combustion raised the temperature of 100 g of water from 293 K to 372 K.

Calculate the standard enthalpy of combustion (ΔH^⦵_c) of the fuel.

The specific heat capacity of water, c = 4.18 J g^-1 K^-1.

Step 1: Calculate heat energy transferred

q = mcΔT = 100 x 4.18 x (372 - 293) = 33,022 J

Step 2: Conversion of J into kJ

To convert from J into kJ, divide by 1,000

33,022 J = 33.022 kJ

Step 3: Calculate number of moles of fuel burnt

n =Mr ​m​=58.01.45​=0.0250 mol

Step 4: Calculate heat released per mole of fuel

ΔHc ⊖​=−nq​=−0.025033.022​=−1320 kJ mol−1

The minus sign indicates this is an exothermic reaction, releasing heat.

Worked example 2 - Calculating standard enthalpy of neutralisation

In a laboratory experiment, 50.0 cm³ of 1.00 mol dm^-3 hydrochloric acid (HCl) at 25.0°C is mixed with 50.0 cm³ of 1.00 mol dm^-3 sodium hydroxide solution (NaOH) also at 25.0°C. The heat formed during this neutralisation raised the temperature of the mixture to 31.5°C.

Calculate the standard enthalpy of neutralisation (ΔH^⦵_neut) of hydrochloric acid.

The specific heat capacity of the mixture, c = 4.18 J g^-1 K^-1.

The density of the mixture, ρ = 1.00 g cm^-3

Step 1: Calculate heat energy transferred

q = mcΔT = (50.0 + 50.0) x 4.18 x (31.5 - 25.0) = 2,717 J

Step 2: Conversion of J into kJ

To convert from J into kJ, divide by 1,000

2,717 J = 2.717 kJ

Step 3: Conversion of cm³ into dm³

To convert from cm³ into dm³, divide by 1,000

50.0 cm³ = 0.0500 dm³

Step 4: Calculate number of moles of HCl used

n = c x V = 1.00 x 0.0500 = 0.0500 mol

Step 5: Calculate heat released per mole of HCl

ΔHneut ⊖​=−nq​=−0.05002.717​=−54.3 kJ mol−1

The minus sign indicates this is an exothermic reaction, releasing heat.