Relative Molecular Mass, the Avogadro Constant, and the Mole
This lesson covers:
- Relative mass
- Calculating relative atomic mass from isotopic abundances
- Determining isotopic abundances from mass spectra
- Defining the mole and Avagadro's constant
- Calculations involving moles
Relative masses
The actual mass of an atom is far too small to measure by weighing. So, the mass of an atom is compared relative to the mass of a carbon-12 atom - this is its relative mass. Relative masses have no units.
You need to know the following definitions:
- Relative atomic mass (Ar) - The weighted mean mass of an atom of an element, compared to 1/12th of the mass of an atom of carbon-12.
For example, chlorine consists of two isotopes - 35Cl (75% abundance) and 37Cl (25% abundance). So its relative atomic mass is the weighted average of 35 and 37, which is 35.5.
- Relative molecular mass (Mr) is the average mass of a molecule compared to 1/12th of the mass of an atom of carbon-12.
For example, a chlorine molecule (Cl2) consists of two atoms of chlorine each with a relative atomic mass of 35.5. So the relative molecular mass of Cl2 is 2 x 35.5 = 71.0
- Relative formula mass (Mr) is the average mass of a formula unit compared to 1/12th of the mass of an atom of carbon-12. Relative formula mass is used for ionic and giant covalent substances.
For example, the formula unit of sodium chloride (NaCl) consists of one sodium atom (Ar = 23.0) and one chlorine atom (Ar = 35.5). So the formula mass of NaCl is 23.0 + 35.5 = 58.5.
Calculating relative atomic mass (Ar)
The relative atomic mass (Ar) of an element is the weighted average mass of all its naturally occurring isotopes.
The steps to calculate relative atomic mass are:
- Multiply each isotope's relative isotopic mass by its isotopic abundance.
- Sum these quantities.
- Divide by the sum of the isotopic abundances.
Worked example 1 - Calculating Ar
Boron has two naturally occurring isotopes:
- 10B has relative isotopic mass 10.0 and abundance 20.0%
- 11B has relative isotopic mass 11.0 and abundance 80.0%
Calculate the relative atomic mass of boron to 1 decimal place.
Step 1: Multiply isotopic mass by isotopic abundance
10B: 10.0 × 20.0 = 200.0
11B: 11.0 × 80.0 = 880.0
Step 2: Sum the quantities
Total = 200.0 + 880.0 = 1,080.0
Step 3: Divide the sum by the sum of the isotopic abundances
Sum of isotopic abundances = 20.0 + 80.0 = 100.0
Ar =100.01,080.0=10.8
Therefore, the calculated relative atomic mass (Ar) of boron is 10.8.
Using mass spectrometry to calculate Ar
Mass spectrometry provides data on the relative abundances of an element's isotopes. This allows the calculation of the relative atomic mass of an element.
The output of a mass spectrometer is a mass spectrum for that element:
- the y-axis of a mass spectrum shows the relative isotopic abundance.
- the x-axis of a mass spectrum shows the mass/charge ratio (m/z), which equals the relative isotopic mass for 1+ ions.
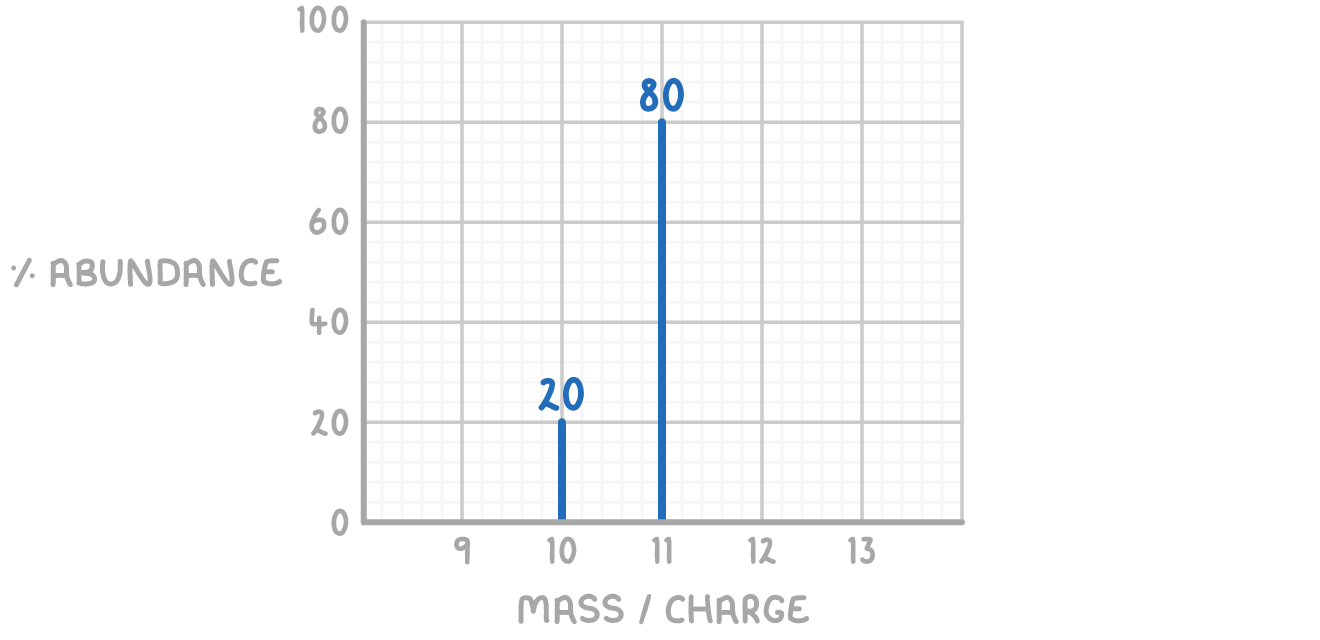
For example, the mass spectrum of boron, shown below, displays two peaks corresponding to its naturally occurring isotopes, 10B and 11B. The height of each peak represents the relative abundance of that isotope, while the m/z value gives the isotope's relative mass.
Worked example 2 - Calculating Ar
The mass spectrum shows neon has three isotopes:
- 20Ne has a relative isotopic mass of 20 and a relative abundance of 57.0.
- 21Ne has a relative isotopic mass of 21 and a relative abundance of 0.1.
- 22Ne has a relative isotopic mass of 22 and a relative abundance of 5.6.
Calculate the relative atomic mass of neon to one decimal place.
Step 1: Multiply isotopic mass by isotopic abundance
20Ne: 20 × 57.0 = 1,140.0
21Ne: 21 × 0.1 = 2.1
22Ne: 22 × 5.6 = 123.2
Step 2: Sum the quantities
Total = 1,140.0 + 2.1 + 123.2 = 1,265.3
Step 3: Divide the sum by the sum of the isotopic abundances
Sum of isotopic abundances = 57.0 + 0.1 + 5.6 = 62.7
Ar =62.71,265.3=20.2
Therefore, the calculated relative atomic mass (Ar) of neon from its mass spectrum is 20.2.
Calculating relative formula mass (Mr)
The relative formula mass (Mr) of a compound is the sum of the relative atomic masses of all the atoms in the compound's formula unit. For molecular compounds comprised of covalently bonded molecules, the term relative molecular mass is used instead of relative formula mass.
The steps to calculate relative formula mass or relative formula mass are:
- Write down the compound's formula unit or molecular formula.
- Identify the number of atoms of each element present in the formula.
- For each element, multiply the number of atoms by its relative atomic mass.
- Sum up the values obtained in step 3.
Worked example 3 - Calculating Mr
Calculate the relative molecular mass of water.
Step 1: Write down the molecular formula
H2O
Step 2: Multipy each element's atom count by its Ar
H: 1.0 × 2 = 2.0
O: 16.0 × 1 = 16.0
Step 3: Calculate Mr
Relative molecular mass = 2.0 + 16.0 = 18.0
Worked example 4 - Calculating Mr
Calculate the relative formula mass of magnesium oxide.
Step 1: Write down the formula unit
MgO
Step 2: Multipy each element's atom count by its Ar
Mg: 24.3 × 1 = 24.3
O: 16.0 × 1 = 16.0
Step 3: Calculate Mr
Relative formula mass = 24.3 + 16.0 = 40.3
The mole
The mole is a convenient unit that allows us to count extremely large numbers of atoms and molecules.
Avogadro's constant has a value of 6.02 x 1023. This very large number represents how many particles are contained in one mole.
The equation linking the number of moles, the number of particles, and Avogadro’s constant is:
number of moles =Avogadro’s constantnumber of particles
where particles refers to atoms, molecules, or ions, electrons.
Worked example 5 - Calculating number of moles
Calculate the number of moles in is 2.71 x 1024 molecules of chlorine.
Avogadro's constant = 6.02 x 1023 mol-1
Step 1: Equation
number of moles =Avogadro’s constantnumber of particles
Step 2: Substitution and correct evaluation
number of moles =(6.02×1023)(2.71×1024)=4.50 mol
Worked example 6 - Calculating number of atoms
Calculate the number of oxygen atoms in a 2.5 moles of oxygen atoms.
Avogadro's constant = 6.02 x 1023 mol-1
Step 1: Rearrange equation
Number of atoms = number of moles × Avogadro's constant
Step 2: Substitution and correct evaluation
Number of atoms = 2.5 × (6.02 × 1023) = 1.5 × 1024 atoms
Relating moles, mass, and molar mass
The molar mass (M) represents the mass in grams of 1 mole of a given substance.
- Molar mass is measured in units of grams per mole (g mol-1).
- Molar mass is numerically equal to relative molecular/formula mass.
The equation linking the number of moles, mass in grams, and molar mass is:
number of moles =molar massmass in g
Or:
n=Mm
Where:
- n = number of moles (mol)
- m = mass (g)
- M = molar mass (g mol-1)
If molar mass (M) is be replaced by relative formula/molecuar mass (Mr), the equation becomes:
n=Mrm
Worked example 7 - Calculating number of moles
Calculate the number of moles in 10.0 g of water (H2O).
Step 1: Calculate Mr of H2O
H: 1.0 × 2 = 2.0
O: 16.0 × 1 = 16.0
Mr = 2.0 + 16.0 = 18.0 g mol-1
Step 2: Equation
n=Mrm
Step 3: Substitution and correct evaluation
n=18.010.0=0.56 mol
Worked example 8 - Calculating mass
Calculate the mass of 7.0 moles of magnesium oxide (MgO).
Step 1: Calculate Mr of MgO
Mg: 24.3 × 1 = 24.3
O: 16.0 × 1 = 16.0
Mr = 24.3 + 16.0 = 40.3 g mol-1
Step 2: Equation
m=n×Mr
Step 3: Substitution and correct evaluation
m= 7.0 × 40.3 = 282.1 g