Measuring Variation

This lesson covers: 

1. Interspecific and intraspecific variation
2. Random sampling
3. Mean, median, and mode
4. Standard deviation and error bars

Interspecific and intraspecific variation

Variation refers to differences between individuals. Generally, variation is due to a combination of genetic and environmental influences.

Interspecific variation:

• This is variation between different species.
• It is due to different genes causing differences in physical traits, adaptations, habitats, etc. and environmental factors like climate, diet, lifestyle, etc.

Intraspecific variation:

• This is variation between individuals within a species.
• It is due to different alleles (gene variants) and environmental factors.

Random sampling

It is often impractical or impossible to measure every single individual when investigating population traits. Random sampling is important to avoid bias and ensure the samples are representative of the whole population.

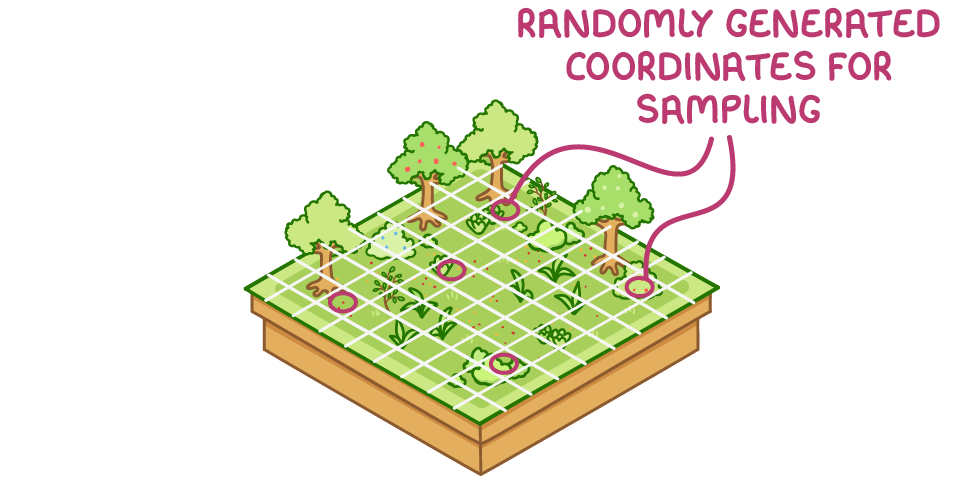
Random sampling involves:

• Randomly generating coordinates across an area to prevent sampling bias.
• Collecting samples from these random coordinates to represent the population.
• Repeating this several times as a large sample size minimises the effects of chance.
• Analysing the data collected to identify any relationships.

Mean, median, and mode

There are three types of average value that can be collected about a sample: the mean, median, and mode.

How to calculate these average values:

1. Mean - The sum of the sampled values divided by the number of values.
2. Median - The central or middle value of a set of values.
3. Mode - The single value of a sample that occurs most often.

Most samples with values either side of the mean will be normally distributed. A normal distribution curve is bell-shaped and symmetrical around a central mean value.

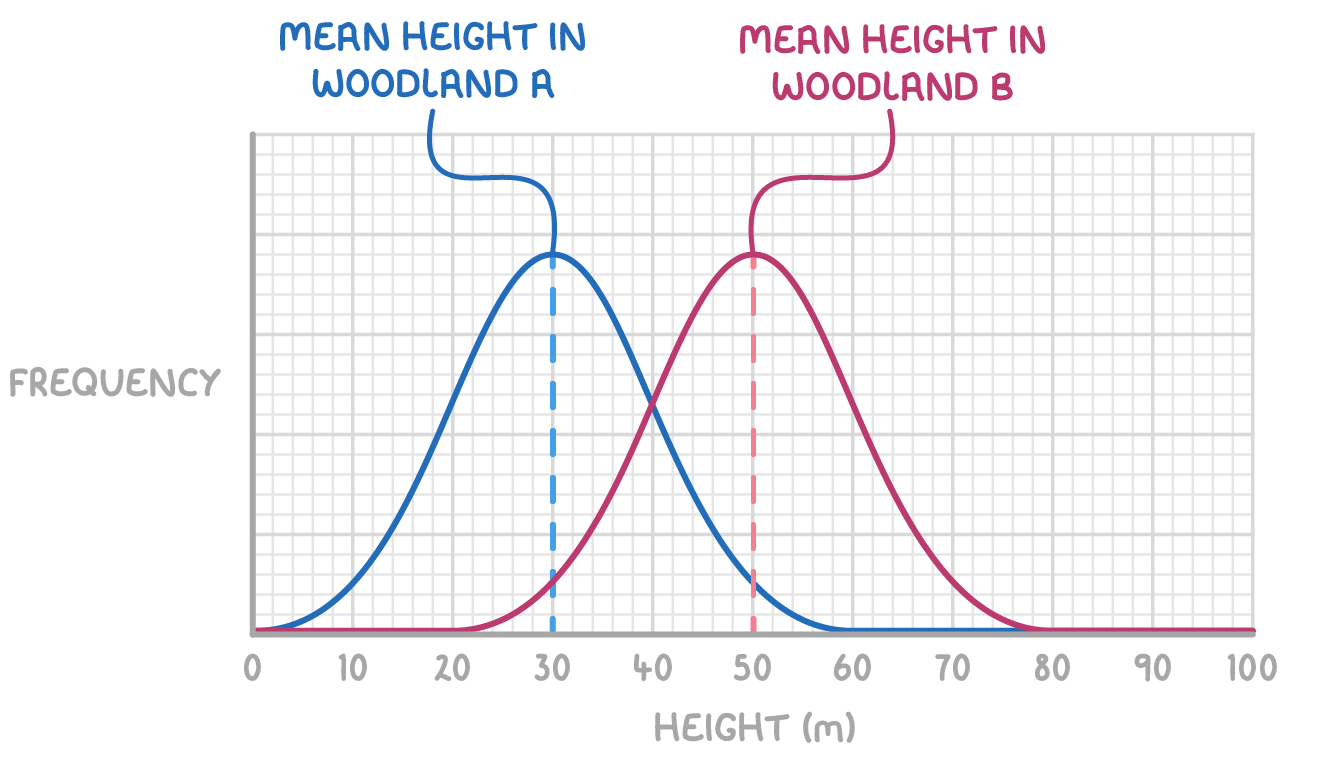
Comparing mean values, shown as the maximum height of the normal distribution curve, helps identify variation between separate samples. 

For example:

• Mean tree height in sample of woodland A = 30 m.
• Mean tree height in sample of woodland B = 50 m.

This 20 m difference shows clear variation between the samples, implying variation between the actual woodland tree populations.

Standard deviation

The standard deviation measures spread of values around the mean within a sample.

How to interpret standard deviation values:

• Small standard deviation - The values are fairly consistent and clustered around the mean.
• Large standard deviation - The values are fairly inconsistent and widely spread around the mean.

The mean height of woodland A in the example above can be represented as 30 m ± 5 m:

• This means that the mean is 30 and the standard deviation is 5.
• Most (~68%) values lie between 25 m and 35 m.

To calculate the standard deviation, we use the following formula (this will be provided):

standard deviation =√n−1Σ(x−xˉ)2​​

Where:

• Σ= the sum of
• x = measured value (from the sample)
• xˉ= mean value
• n = total number of values in the sample

Error bars

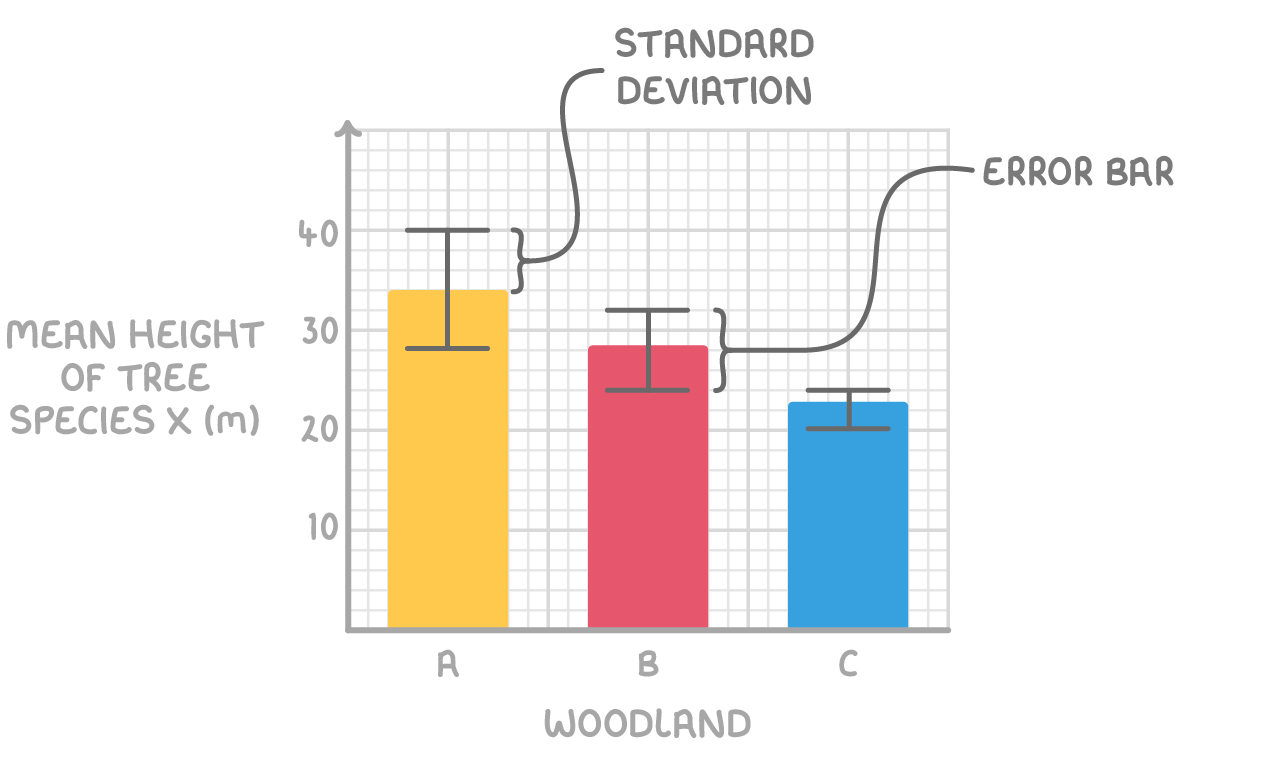
Error bars display the standard deviation visually:

• They are plotted one standard deviation above and below the mean.
• The error bar length shows degree of value spread in the sample.
• Longer error bars indicate more variation around the mean within that sample.

Worked example - Quantifying tree height variation using standard deviation

Calculate the standard deviation of tree heights in a sample from woodland A using the following data collected for tree heights: 32 m, 35 m, 31 m, 29 m, and 33 m.

Step 1: Equation

standard deviation =√n−1Σ(x−xˉ)2​​

Step 2: Calculate the mean (xˉ)

xˉ=nsum of all tree heights​

xˉ=532+35+31+29+33​

xˉ=5160​=32

Step 3: Calculate (x−xˉ)2 for each tree height

for each tree height, subtract the mean and square the result

(x1​−xˉ)2=(32−32)2=0

(x2​−xˉ)2=(35−32)2=9

(x3​−xˉ)2=(31−32)2=1

(x4​−xˉ)2=(29−32)2=9

(x5​−xˉ)2=(33−32)2=1

Step 4: Summation and division

sum all squared differences and divide by n−1

Σ(x−xˉ)2=0+9+1+9+1

Σ(x−xˉ)2=20

n−1Σ(x−xˉ)2​=5−120​

n−1Σ(x−xˉ)2​=420​=5

Step 5: Square root the value from step 4

take the square root of this value to get the standard deviation

standard deviation =√5≈2.24 m (to 3 s.f.)